Research topics
My research interests lie at the intersection of statistical signal processing and machine learning, and how they have synergistic effects on system monitoring. Specific interests include adaptive signal processing, distributed optimization, kernel methods, hyperspectral image processing and bioinformatics. I work with several worldwide first-class professors on these topics.
Featured work - Diffusion adaptation over multitask network
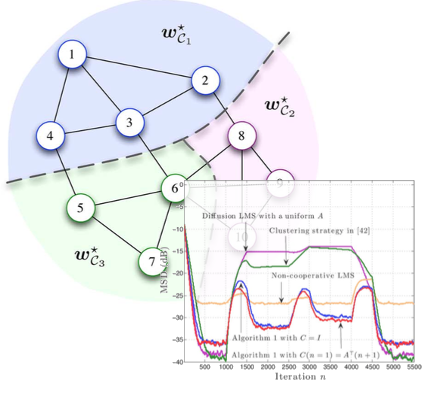
Adaptive networks are suitable for decentralized inference tasks. Recent works have intensively studied distributed optimization problems in the case where the nodes have to estimate a single optimum parameter vector collaboratively. However, there are many important applications that are multitask-oriented in the sense that there are multiple optimum parameter vectors to be inferred simultaneously, in a collaborative manner, over the area covered by the network. We introduced the multitask adaption into distributed networks. We chareacterized the performance of single-task algorithms performed in multitask enviroments, employed diffusion strategies to develop distributed algorithms that address multitask problems by minimizing a cost with appropriate regularizations among node clusters, and also proposed an efficent combination coefficient adjustment rule for node clustering.
Featured work - Constrained and nonlinear adaptive filter design and analysis
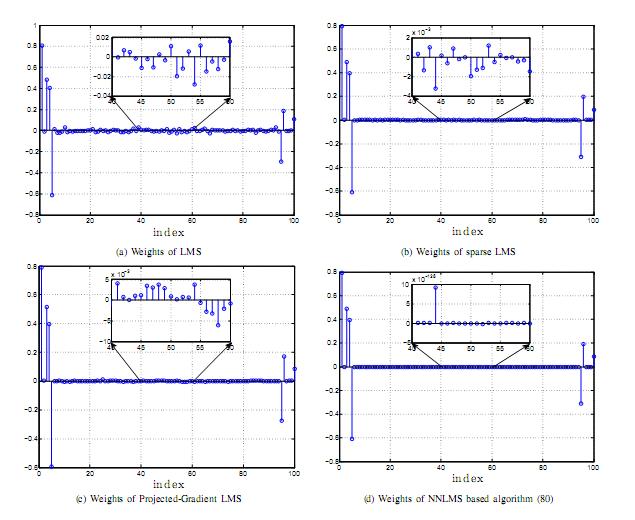
Constraints and nonlinearities play an important role in morden signal processing problems. Due to the inherent physical characteristics of systems under investigation, some constraints are desired to be imposed on the parameters to estimate. We have designed and analyzed online algorithms for addressing the non-negativity constraints and L1-norm constraints with streaming data. Besides, adaptive filtering algorithms operating in reproducing kernel Hilbert spaces have demonstrated superiority over their linear counterpart for nonlinear system identification. We are interested in studying online nonlinear system identification algorithms with sparse dictionary, and providing analytical conditions for their stochastic convergence behavior.
Featured work - Nonlinear hyperspectral data analysis
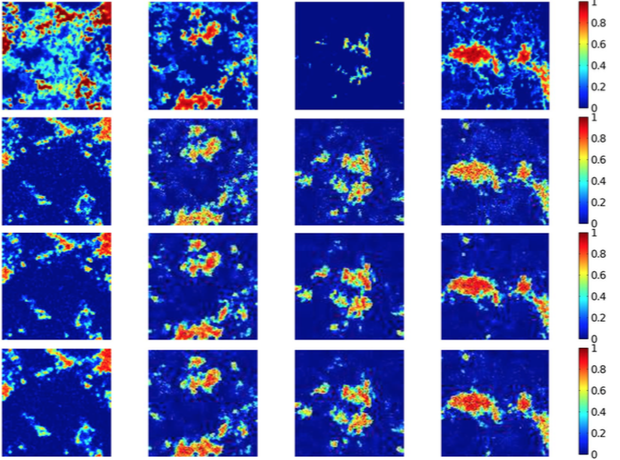
Spectral unmixing is an important issue to analyze remotely sensed hyperspectral data. Although the linear mixture model has obvious practical advantages, there are many situations in which it may not be appropriate and could be advantageously replaced by a nonlinear one. We formulate a new kernel-based paradigm that relies on the assumption that the mixing mechanism can be described by a linear mixture of endmember spectra, with additive nonlinear fluctuations defined in a reproducing kernel Hilbert space. This family of models has clear interpretation, and allows to take complex interactions of endmembers into account. Extensive experiment results, with both synthetic and real images, illustrate the generality and effectiveness of this scheme compared with state-of-the-art methods. Considering that integrating spatial information into hyperspectral unmixing procedures has a positive effect on the estimation of fractional abundances due to the inherent spatial-spectral duality in hyperspectral scenes, we also investigated how to incorporate spatial correlation into a nonlinear abundance estimation process.
Featured work - Network methods applied to bioinformatics research
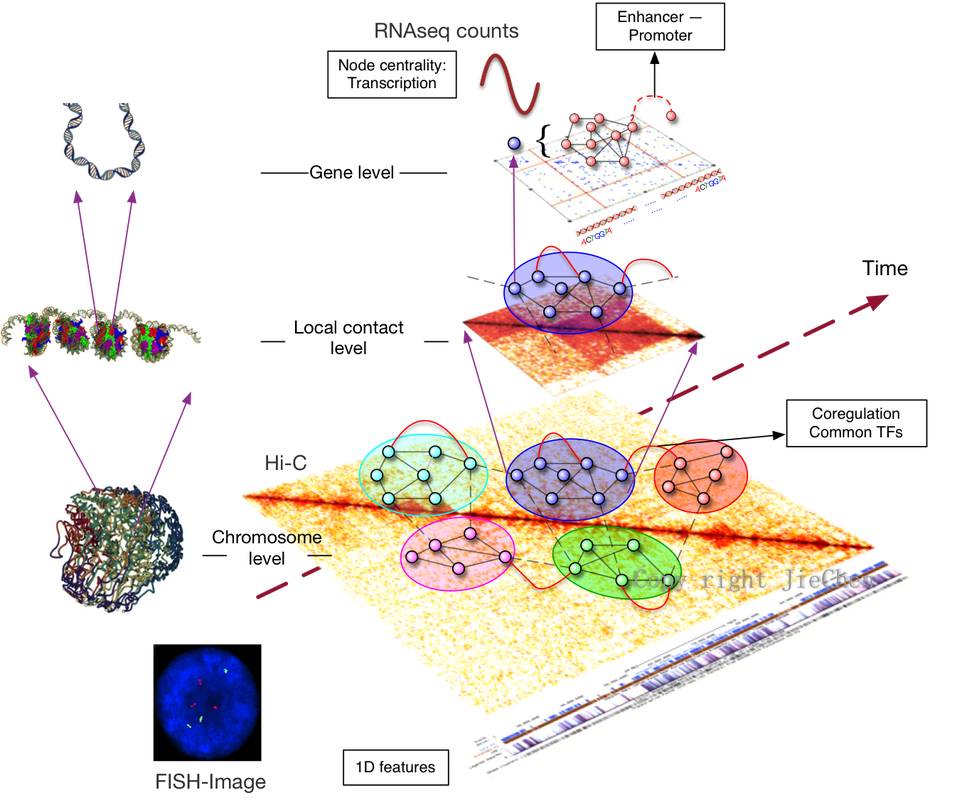
The four-dimensional organization of the interphase nucleus, or the 4D nucleome (4DN), reflects the dynamical interaction between form and function in the genome and its impact on phenotype. We performed an initial characterization of the human 4DN. Over a time series, form is captured through genome-wide chromosome conformation capture (Hi-C) and through 3D imaging (FISH). Genome-wide gene expression—transcription—is captured by RNA-seq as a measure of genome function. We established a data-guided unified mathematical framework based on the graph Laplacian for quantification of the relationship between form and function on multiple genome scales. A series of new methods are proposed for tasks including compartment A/B determiniation, topological domain extraction, adaptive resolution Hi-C matrix generation, gene structure characterization and gene expression clustering etc.
jie-chen.com
I am a professor, and Vice Dean of "Center of Intelligent Acoustics and Immersive Communications" (CIAIC) at School of Marine Science and Technology of Northwestern Polytechnical University, China I am an expert of "thousand youth talents plan" of China. From Apr. 2014 to Mar. 2015, I worked at Department of Electronic Engineering and Computer Science of University of Michigan (Ann Arbor, US) with Prof. Alfred O. Hero and Prof. Indika Rajapakse.
犀利士
在使用犀利士前,先與您的醫生分享您生活中的其他問題 談論您的健康意味著分享有關您的身體、情感和精神感受的資訊。知道如何描述您的癥狀並提出其他問題將説明您成為醫療保健的合作夥伴。
使用這些工作表在與醫生交談時組織您的問題和資訊。